Significance
Scientists and managers alike have been preoccupied with the question of whether and, if so, under what conditions groups of interacting problem solvers outperform autonomous individuals. Here we describe an experiment in which individuals and groups were evaluated on a series of tasks of varying complexity. We find that groups are as fast as the fastest individual and more efficient than the most efficient individual when the task is complex but not when the task is simple. We then precisely quantify synergistic gains and process losses associated with interacting groups, finding that the balance between the two depends on complexity. Our study has the potential to reconcile conflicting findings about group synergy in previous work.
Abstract
Complexity—defined in terms of the number of components and the nature of the interdependencies between them—is clearly a relevant feature of all tasks that groups perform. Yet the role that task complexity plays in determining group performance remains poorly understood, in part because no clear language exists to express complexity in a way that allows for straightforward comparisons across tasks. Here we avoid this analytical difficulty by identifying a class of tasks for which complexity can be varied systematically while keeping all other elements of the task unchanged. We then test the effects of task complexity in a preregistered two-phase experiment in which 1,200 individuals were evaluated on a series of tasks of varying complexity (phase 1) and then randomly assigned to solve similar tasks either in interacting groups or as independent individuals (phase 2). We find that interacting groups are as fast as the fastest individual and more efficient than the most efficient individual for complex tasks but not for simpler ones. Leveraging our highly granular digital data, we define and precisely measure group process losses and synergistic gains and show that the balance between the two switches signs at intermediate values of task complexity. Finally, we find that interacting groups generate more solutions more rapidly and explore the solution space more broadly than independent problem solvers, finding higher-quality solutions than all but the highest-scoring individuals.
Tasks performed by groups of interacting problem solvers—whether in the real world or in experimental settings—vary along a number of dimensions that plausibly influence group performance (1⇓⇓⇓⇓–6). In this paper, we focus on an important but empirically understudied dimension of tasks, complexity, which is generally understood to depend on at least two factors: (i) the number of distinct components that constitute a task and (ii) the number, strength, and configuration of interdependencies between those components (7⇓⇓⇓–11).
Intuitively, task complexity is of obvious relevance to group performance. All else equal, one would expect problem solvers to perform worse on tasks that have more components or for which the interactions between components are more dense. In addition, one might also expect task complexity to impact group “synergy,” defined as performance in excess of what would be expected for a similarly sized collection of individuals working independently—aka “nominal group” (12). In this case, however, it is less obvious what the direction of the effect would be. On one hand, interacting groups might perform better relative to nominal groups on complex tasks because they are able to distribute effort (13), share information about high-quality solutions (14), or correct errors (15). On the other hand, with more complex tasks, interacting groups might experience even greater process losses—including social loafing (16), groupthink (17), and interpersonal conflict (4)—possibly because complex tasks place greater demands on individual contributors and offer more opportunities to get stuck in globally suboptimal local optima, either of which could also lead to increased stress and underperformance relative to nominal groups.
A major challenge to resolving questions about the effects of task complexity is that while the high-level concept seems intuitive, it has not yet been operationalized precisely enough to allow researchers to quantify the complexity of different types of tasks and hence make apples to apples comparisons between them. Rather, existing operationalizations are often themselves complex. For instance, one model lists 27 complexity contributing factors grouped under 10 complexity dimensions (9), while other models are sufficiently domain-specific that numerical differences between different types of tasks are hard to interpret (7). Adding confusion, some definitions emphasize objective complexity, referring only to task features that can be measured independently of those performing a task, whereas others emphasize subjective complexity, the task’s complexity as experienced by those doing it (9, 11).
Here we avoid these analytical difficulties by identifying a class of tasks for which complexity can be varied systematically while keeping all other elements of the task fixed. In this way, we can easily measure performance as a function of increasing complexity without worrying about confounds arising from other aspects of the task such as task type (3) or other features of group processes (4, 18). In addition, we require that our tasks can realistically be performed either independently or collaboratively, thereby allowing for straightforward comparison between nominal and interacting groups.
A class of tasks that satisfy these criteria are constraint satisfaction and optimization problems (CSOPs), which are widely studied in artificial intelligence and operations research. The connection to operations research is useful because unlike other “toy” problems, CSOPs map in a relatively intuitive way to a range of practical resource allocation problems and have been used to model many problems that are of practical interest. Examples of CSOPs include staffing software projects where there are several potential developer-to-activity assignments to evaluate (19); forming learning groups based on some criteria related to the collaboration goals (20); railway timetabling (21); and allocating vaccines, ventilators, and medical supplies during the COVID-19 pandemic (22). Furthermore, while CSOPs capture important features of real-world group problem-solving exercises, they do not require participants to have specialized skills. As a result, participants can be recruited from online services, reducing the cost and difficulty of coordinating simultaneous participation of groups. Finally, as with other complex problems (14, 23⇓–25), the payoff function for CSOPs can be described as a rugged performance landscape, where each point on the landscape represents a combination of potentially interdependent choices (a solution to the problem), while the height of the point represents the performance of that combination (26, 27). Therefore, CSOPs can be characterized by several locally optimal but globally suboptimal solutions (26, 27) and so are amenable to potentially many solution strategies and styles, with no single universally superior strategy (28).
The specific CSOP that we studied is a room assignment problem in which participants—either as individuals or in groups—assign N students to M rooms where each student has a specified utility for each room (SI Appendix, section 1.1). The task’s goal is to maximize the total student utility while also respecting Q constraints (e.g., “Students A and J may not share a room or be in adjacent rooms”). When the task is done in groups, participants are allowed to communicate via text-based chat and to move different students simultaneously, thereby performing parallel processing if they chose to. Critically for our purposes, the task complexity can be varied systematically by adjusting just three key parameters: the number of students , the number of rooms , and the number of constraints . Indeed, a significant advantage of this task (and CSOPs in general) over tasks that are more commonly studied in group performance settings is that its complexity can be quantified in terms of the run time required by an algorithmic solver to find the optimal solution, allowing us to easily rank task instances by complexity (see Materials and Methods for more details). Fig. 1 illustrates how complexity can be varied between two instances of the room assignment problem. In a low-complexity instance, six students must be assigned to four rooms subject to only two constraints (“B and E must be neighbors” and “C and F can’t live in the same room”). In a high-complexity instance, 18 students must be assigned to 8 rooms subject to 18 constraints.
Illustration of the room assignment task. The task required assigning N students to M rooms so as to maximize the total utility of the students, who each have a specified utility for each room, while also respecting Q constraints. The complexity of the task is characterized by the number of students to be assigned , the number of dorm rooms available , and the number of constraints . (Top) A low-complexity case in which six students are to be assigned to four rooms subject to two constraints. (Bottom) A high-complexity case in which 18 students are to be assigned to 8 rooms subject to 18 constraints. See SI Appendix, section S1.1, for details and SI Appendix, Figs. S1–S2, for screenshots of the task interface.
Experiment Design
In this paper, we test the hypothesis that task complexity moderates the relative performance of group-vs.-individual problem solving. To this end, we address the following question: how does the balance between process losses and synergistic gains in interacting groups depend on task complexity?
Our experiment proceeded in two phases. In phase 1, 1,200 participants individually completed five room assignment tasks: three very low– and two moderate-complexity tasks (SI Appendix, Table S1) as well as a standard Reading the Mind in the Eyes test (SI Appendix, section S1.2 and Fig. S3), which is commonly used as a measure of social perceptiveness and was used by several recent studies relating social perceptiveness to group performance (18, 29⇓⇓–32).
After the completion of phase 1, we scored all participants on skill level and social perceptiveness so that we could assign them to experimental blocks in phase 2 (SI Appendix, section 1.4 and Fig. S4). By accounting for these features in our block-randomization procedure in phase 2, we could ensure that various levels of skill and social perceptiveness (and combinations thereof) were balanced across the group and individual work arrangements. The main purpose of the block-randomization scheme was to oversample statistically less frequent combinations (e.g., all group members having high skills or high social perceptiveness), thereby increasing the statistical power of our experiments. We note that our focus here is on the comparison between interacting and nominal groups, not on compositional differences between interacting groups; thus, our analysis of the effects of skill level and social perceptiveness on performance will be published elsewhere (as per our preregistration).
The same 1,200 participants were invited to participate in phase 2, and the first 828 participants who showed up and passed the attention checks (as per our preregistration; see SI Appendix, Table S2, for sample sizes) were assigned to a second sequence of five room assignment tasks (task sequence was randomized), also of varying complexity (very low, low, moderate, high, and very high; SI Appendix, Table S3 and Fig. S5). All tasks timed out at 10 min in phase 2, regardless of complexity. Based on each participant’s skill and social perceptiveness as measured in phase 1, we first assigned each individual into blocks (e.g., high skill, high social perceptiveness; mixed skill, high social perceptiveness; etc.). Next, within each block, participants were randomized to one of two conditions: an interacting group condition ( participants, forming 197 groups of size 3; data for 1 group are incomplete, leading to the number of valid interacting groups being 196), in which group members solved the problem collectively and could communicate with each other via text-based chat; and an independent individual condition ( participants; data from 3 individuals are incomplete, leading to the number of valid independent individuals being 234), in which each participant worked on their assigned task alone. All results presented herein are from phase 2 of the experiment.
Performance Evaluation.
In phase 2, we used three metrics to capture performance in a room assignment task instance: (1) normalized score, defined as the actual score obtained in a task instance divided by the maximum possible score for that task; (2) duration (or time to completion), defined as the time elapsed from the start of the task until a solution was submitted (or until the task times out at 10 min); and finally, (3) efficiency, defined as the normalized score divided by the duration.
All three metrics are natural indicators of performance which one may wish to optimize under some circumstances. In the absence of time constraints, for example, normalized score is an obvious measure of solution quality. By contrast, duration is appropriate when the problem-solving time is more important than quality (e.g., quickly come up with a reasonably good plan for resource allocation in a disaster response), and efficiency is appropriate when both quality and speed are important (e.g., in product development).
Following prior work (12, 33⇓⇓⇓–37), we evaluate group performance in comparison with so-called nominal groups, defined as a similarly sized collection of autonomous individuals. Nominal groups provide a useful benchmark for interacting groups because they account for differential resource availability between groups and individuals (12); that is, they adjust for the amount of intellectual resources that groups could bring to bear (i.e., labor hours) and the mathematical probability that at least one member could have achieved the same performance. Thus, interacting group performance over and above that of a nominal group can be attributed to the group interaction, not greater resources.
In general, comparisons between interacting groups and equivalently sized nominal groups have found mixed evidence for synergistic effects (12): while interacting groups often outperform the average member of a nominal group (weak synergy), they rarely outperform the best member (strong synergy). Reflecting this distinction, we compare our interacting groups with four performance benchmarks, each corresponding to a distinct nominal group constructed by drawing three individuals randomly and without replacement from the same block. The first benchmark corresponds to the performance score for a randomly chosen member of the nominal group (equivalent to an average individual), while the remaining three correspond to the individual with the best phase 1 performance on each of the three metrics defined above (i.e., highest score, lowest duration, and highest efficiency). Nominal groups, therefore, simulate a situation in which a manager assigns the work to either a random individual, the highest-scoring individual, the fastest individual, or the most efficient individual, as judged by past performance (i.e., phase 1 scores, durations, and efficiencies).
Results
Performance as a Function of Task Complexity.
Fig. 2 shows how performance varied as a function of task complexity. Across all conditions, higher task complexity resulted in lower normalized scores (Fig. 2A), longer duration (Fig. 2B), and hence lower efficiency (Fig. 2C). These performance trends also hold when measured separately for interacting and nominal groups (SI Appendix, section S2 and Fig. S7). On average, individuals and groups spent roughly three times as long on the most complex task than on the least complex task, but obtained normalized scores that were roughly 10 percentage points lower. Given that normalized scores were almost always in excess of 80, this last difference represents roughly 50% of the effective range—a large effect. The clear monotonic dependency of all three performance measures on complexity is important for two reasons. First, it validates our design, demonstrating that increases in complexity as captured by changes in the task parameters N, M, and Q translate in a straightforward way to complexity experienced by our participants. Second, it offers considerable leverage to test our prediction that the relative performance of interacting groups versus nominal groups depends upon task complexity.
Varying the room assignment task complexity. Increasing the task complexity (A) reduces the normalized score, (B) increases the time required to complete the task, and (C) reduces efficiency. Data are combined across both individual and group conditions across all six blocks. Error bars indicate the 95% confidence intervals (some are not large enough to display). Groups and individuals scored at least 80% of the maximum score in over 85% of tasks; hence, the effective range for the normalized score (i.e., the y axis of A) is between 80 and 100%. The minimum time required for a solution to be submitted is 1 min, and the maximum is 10 min; hence, the effective range for the duration (i.e., the y axis of B) is between 1 and 10 min. The difference in experienced difficulty between very low and very high complexity is very large: the average normalized score dropped by about 50% of the effective range of scores (from roughly 95 to 85% on an effective scale of 80 to 100), and the average time taken increased by 200% (from 2 to 6 min).
Evidence for Group Synergy.
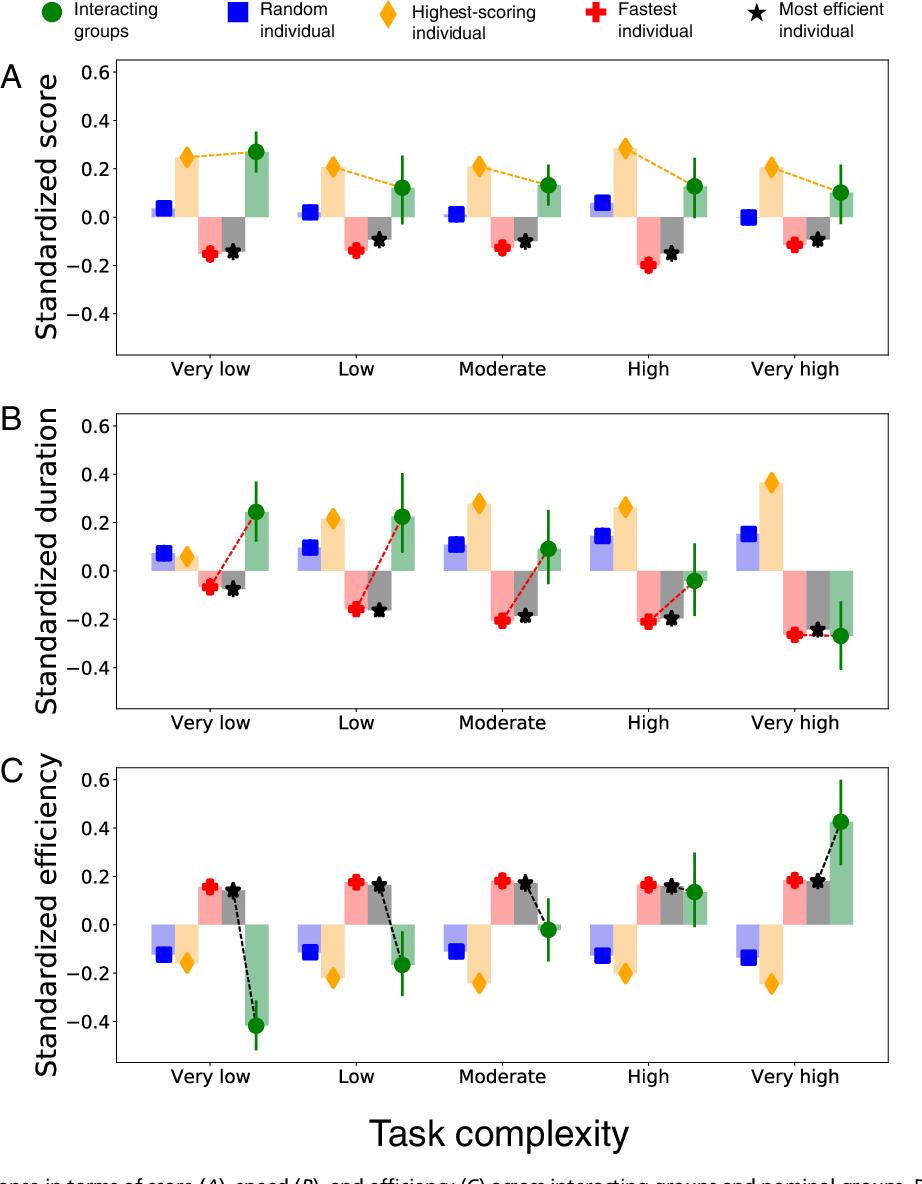
Fig. 3 compares overall standardized group performance (transformed to z scores within each task complexity level) with the four nominal group definitions: random individual, highest-scoring individual, fastest individual, and most efficient individual.
Comparing performance in terms of score (A), speed (B), and efficiency (C) across interacting groups and nominal groups. Data are combined across all six blocks and standardized (i.e., transformed to z scores) within each task complexity level (differences are relative within the complexity level and should not be compared across complexity levels). Error bars indicate the 95% confidence intervals. We have repeated the analyses presented in this figure for each block, with qualitatively similar results (SI Appendix, section S3 and Figs. S8–S10).
Performance as solution quality.
For all levels of task complexity, Fig. 3A shows that groups score higher than the random selected, fastest, and most efficient members of equivalently sized nominal groups (P = 0.013, 95% CI [0.026, 0.225]; P < 0.001, 95% CI [0.184, 0.410]; P < 0.001, 95% CI [0.155, 0.378]; respectively) but lower than the highest-scoring member (P = 0.047, 95% CI [−0.159, −0.001]; see SI Appendix, Tables S4–S7, for regression tables). This result is consistent with longstanding findings (33⇓⇓⇓–37) that interacting groups often outperform nominal groups in terms of solution quality when the standard is set by an average-member criterion (weak synergy), but not when it is set by a best-member criterion (strong synergy).
Performance as speed.
Fig. 3B shows that interacting groups complete more complex tasks—but not simpler ones—faster than both the random and highest-scoring members of equivalently sized nominal groups. Moreover, interacting groups are as fast as the fastest and most efficient members at the highest task complexity (see SI Appendix, Tables S8–S10, for regression tables). These suggest that indeed, for tasks with many components (students and rooms) and dense interdependencies (many constraints), the benefits of distributing work to a group might outweigh the process losses associated with interacting groups, which is consistent with findings in prior work (36).
Performance as efficiency.
Finally, Fig. 3C shows that for the most complex tasks the gains in speed exceed the deficits in the score. This results in a striking interaction between task complexity and work arrangement: while interacting groups are considerably less efficient than selected members of nominal groups on simple tasks, their relative efficiency increases with task complexity until they surpass the highest-scoring, fastest, and most efficient members at the highest complexity (see SI Appendix, Tables S11–S13, for regression tables). This result is reminiscent of group decision-making among social insects wherein a recent study has found that ant colonies outperform individual ants when the discrimination task is difficult but not when it is easy (38).
Unpacking Group Synergy.
The finding that interacting groups are more efficient than the best selected members of equivalently sized nominal groups—by any of our four definitions—when the task is complex, but not when the task is simple, suggests that the balance between process losses and synergistic gains does depend on task complexity. To better understand this dependency, and noting that the variation in efficiency apparent in (Fig. 2C) is more dependent on variation in task duration (which varies between 2 and 6 min on average, Fig. 2B) than on variation in the score achieved (which varies between 95% and 85% on average, Fig. 2A), we next present an exploratory analysis of the time spent in each stage of solving the task. This analysis is made possible by the highly granular nature of our data. Because every action taken by every participant is timestamped, we can partition the overall solution time into very precisely measured segments that correspond to distinct stages of the problem-solving process. For clarity, we define four key segments, illustrated schematically in Fig. 4A:
Task completion milestones. (A) The four milestones in the problem-solving process: (i) the first intermediate solution is generated, (ii) the best intermediate solution is generated, (iii) the final solution is generated, and (iv) the final solution is submitted. (B, D, F, and H) The time spent (in minutes) by groups and individuals (whether random, highest-scoring, fastest, or most efficient) in each time segment. (C, E, G, and I) The standardized time spent (transformed to z scores; i.e., showing the relative difference within complexity level) in each time segment. Error bars indicate the 95% confidence intervals.
Time to first solution, .
The time from the beginning of the task to generating the first solution can be viewed as time spent in formulating a strategy to approach the task.
Time to best solution, .
The best solution is not necessarily the one submitted because the task instance only ends once a group/individual decides to submit a solution, and groups/individuals may generate solutions after their best solution without returning to it.
Time from best to final solution, .
The time spent between generating the best and final solutions, which can be viewed as “excess exploration,” decreases efficiency as it leads to lower (or equal) solution quality but greater total task duration.
Time from the final solution to submission, .
The time spent between generating the final solution and deciding to submit it, which can be viewed as “commitment time,” can be another source of inefficiency as it leads to equal solution quality but increases the total task duration.
Fig. 4 shows two sets of comparisons between interacting and nominal groups for each of these four segments. Fig. 4 B, D, F, and H show the raw durations for , , , and , respectively, for interacting groups (green) along with the four previously defined nominal group benchmarks (random member, highest-scoring member, fastest member, and most efficient member), while Fig. 4 C, E, G, and I show the same results as standardized durations. We make five main observations about Fig. 4.
First, we observe that (on average) interacting groups spend less time in (time to first solution, Fig. 4 B and C) than the members of nominal groups regardless of task complexity ( for all; and SI Appendix, Table S14). We speculate that this observation may be related to arguments from recent studies that group membership reduces the sense of responsibility and regret that members may face under the same circumstances individually. If correct, a reduced emotional barrier to action may be an underlying mechanism driving group members to act earlier (39).
Second, we observe a noticeable effect of task complexity on (time to best solution, Fig. 4 D and E): interacting groups are slower to reach their best-found solution than the fastest and most efficient members of nominal groups for the least complex task but faster for the most complex task (P < 0.001, 95% CIs [0.119, 0.385] and [0.109, 0.371], respectively, at the lowest complexity, and P < 0.001, 95% CIs [−0.351, −0.085] and [−0.370, −0.108], respectively, at the highest complexity; see SI Appendix Tables S17–S18 for regression tables). Importantly, we note that most of the task duration is spent in this segment, suggesting that speed to best solution is the main contributor to group synergy. One potential explanation for why interacting groups are faster at finding the best solution at high complexity is that interacting groups realize some benefits of division of labor (see SI Appendix, section S4 and Fig. S11, for suggestive evidence). Another possible explanation, for which we see some anecdotal evidence in the chat logs (SI Appendix, Fig. S11), is that interacting groups are more willing to satisfice by accepting a currently available solution as satisfactory (40). Yet another could be that they benefit from turn-taking, wherein one person is primarily active, while the others are considering their next move(s). Unfortunately, the current experiment design does not allow us to discriminate between these alternative explanations, hence they remain speculative.
Third, we observe that regardless of complexity, interacting groups spend more time in (excess exploration, Fig. 4 F and G) segment relative to the members of nominal groups; as with , the difference is consistent across levels of complexity (see SI Appendix, and Tables S19–S20 for regression tables). Fourth, interacting groups also spend more time to commit to a solution () than the selected members of nominal groups, once again regardless of complexity (Fig. 4 H and I and SI Appendix, Table S14). We speculate that the fact that interacting groups can communicate via chat (and lack an assigned leader) may add pressure to groups to ensure that their decisions are made collectively (i.e., reaching consensus), which could contribute to the observed effect.
Fifth, we observe that the mean total task duration ranges from min at very low complexity to min at very high complexity (out of a maximum of 10 min), meaning that participants generally submit the solution and end the task instance before running out of time. This observation is relevant to our analysis in that our performance comparisons of interacting groups to that of selected members of nominal groups is unaffected by the time constraint.
Summarizing, Fig. 4 reveals two types of process losses (i.e., the extra time spent in excess exploration and achieving consensus) and two types of synergies (i.e., faster time to first solution and faster time to best solution for complex tasks). Interestingly, whereas the synergies—specifically in the time to best solution—depend on task complexity, the process losses do not. In other words, our findings suggest that being in an interacting group has fixed costs that are relatively consistent across task complexity levels but a benefit that varies across complexity levels (i.e., less time spent to find the best solution).
To further clarify this finding, we next aggregate the costs and benefits to quantify the value of performing the task in an interacting group across complexity levels. In particular, we measure each cost and benefit as the absolute difference, in terms of time spent, between interacting groups and the random (i.e., average) member of nominal groups in each time segment:
Fig. 5 shows that the total cost associated with interacting group inefficiencies (i.e., excess exploration, reaching consensus) exceeds the synergistic benefits (i.e., speed gains in finding the best solution) when solving low-complexity tasks but not high-complexity ones. This explains our finding that groups are more efficient than the highest-scoring, fastest, and most efficient members of equivalently sized nominal groups when the task is complex but that this relationship is reversed when the task is simple. We find similar results for the highest-scoring member comparison (SI Appendix, section S5 and Fig. S12).
The cost-benefit of interacting groups. The figure illustrates the absolute difference in terms of average time spent between interacting groups and an average individual nominal group in each time segment.
Exploring Differences in Problem-Solving Approaches.
Recapping our main results, interacting groups are more efficient than even the most efficient member of nominal groups for high-complexity problems; hence, we conclude that they display strong synergy for efficiency (Fig. 3C). Regarding speed, interacting groups are faster than the average (randomly chosen) member and as fast as the fastest member of equivalently sized nominal groups (Fig. 3B), thereby displaying only weak synergy. For solution quality, interacting groups display even weaker synergy as they score higher than the average member but not quite as well as the highest-scoring member of nominal groups (Fig. 3A).
To further investigate these results, we examined the number and pace of generated intermediate solutions, where an intermediate solution is defined as an assignment of students to rooms (i.e., each action taken by a participant generates an intermediate solution). As shown in Fig. 6 A and B, we observe that groups not only generated more intermediate solutions than the random, highest-scoring, fastest, and most efficient members of equivalently sized nominal groups ( for all, 95% CIs , , , and respectively; SI Appendix, Table S23); they did so at a higher rate as well ( for all, 95% CIs , , , and , respectively; SI Appendix, Table S23). Interacting groups also exhibited a wider solution radius, defined as the maximum edit distance (i.e., the number of differences in student/room assignments) between the first complete solution (i.e., all students assigned to rooms but conflicts may be unresolved) and all subsequent complete solutions, suggesting they explored the solution space more broadly (Fig. 6C; for all, 95% CIs , , , and respectively; SI Appendix, Table S23). We also confirmed this qualitative conclusion using two other measures of exploration: the percentage of solutions within an edit distance of two of the final solution and the percentage of intermediate solutions that involved a constraint violation (SI Appendix, Figs. S13 and S14).
Mechanistic differences in problem-solving approaches between interacting groups and individuals. Interacting groups generate (A) more solutions, (B) at a faster rate, and (C) explore the solution space more broadly. (D) However, the quality of the best-found solution (whether submitted or not) is not better than the solution found by the highest-scoring-individual nominal groups. Error bars indicate the 95% confidence intervals.
In light of these observations, it is all the more surprising that interacting groups did not find higher-quality solutions than the highest-scoring member of nominal groups (Fig. 6D; ; SI Appendix, Table S23). In part the gap can be explained by interacting groups also failing to submit their best-found solution at a higher rate than the highest-scoring individual: across all complexities, the highest-scoring individual fails to submit their best-found solution of the time, whereas interacting groups fail to submit their best solutions of the time (; difference in proportions). As a result, interacting groups’ submitted solutions were worse relative to highest-scoring individual members than if everyone had submitted their best-found solution (compare Fig. 3A with Fig. 6D), although even then some gap remains.
What might account for the combination of strong synergy in efficiency and only weak synergy for solution quality and speed? Prior research that conceptualizes problem solving as an adaptive search on a rugged performance landscape (14, 27), wherein each point on the landscape represents one solution to the room assignment and the height of the point represents the performance of that assignment, provides several, possibly interrelated, explanations. One potential explanation is that the highest-scoring individuals have better representations (lower-dimensional approximations) of the true performance landscape, which allows them to evaluate solutions (and solution trajectories) offline without testing them through experimentation (41, 42). Better representations can lead to more accurate offline evaluations and more effective search efforts (26, 43, 44), characterized by fewer intermediate solutions and higher solution quality. Alternatively, groups of problem solvers might have conflicting interests (e.g., maximizing score vs. minimizing duration) and, hence, different visions of the right course of action (45). If true, groups might benefit from central coordination by assigning a group leader (45) or from process-related interventions like enforcing intermittent breaks in interaction (46, 47). Yet another possibility is that when time is limited, search strategies that allow for quick wins (i.e., steep performance improvements early on) and reduce the amount of exploration might appear superior (26). Therefore, while the local path-deepening search strategy (e.g., hill climbing) adopted by the highest-scoring members of equivalently sized nominal groups might provide short-run performance benefits, the interacting groups’ strategy of broadening the search domain might be more advantageous in the long run (48, 49).
Discussion
For many tasks of interest, managers can decide whether to assign a task to an interacting group or to a comparable number of individuals working independently (12). For settings such as these, our results offer several insights. First, decisions about how to allocate work—to interacting groups or to nominal groups—should depend on the complexity of the task at hand and the way performance is evaluated. For example, if a manager wanted to find a workable solution to a CSOP in the least amount of time, the recommendation would be to ask a group to solve the problem when the problem is complex but to ask independent problem solvers when it is simple. It is noteworthy that the duration and efficiency results presented here may actually underestimate how this would work in practice. For instance, if the work was organized in nominal groups, that arrangement would still produce multiple different solutions for some manager to decide between. Although our operationalization of nominal groups simulated a situation in which the manager makes the decision instantaneously, there are circumstances where a manager might want to consider the merits of the different solutions, and this would take a nonzero amount of time. This is not the case with interacting groups, where the decision process is already included in the elapsed time of the problem-solving exercise.
Second, our findings also suggest that a possible explanation for why group process losses have figured more prominently in research findings than synergistic gains (12) is that laboratory studies of group performance generally rely on very simple tasks. Indeed, the clearest laboratory evidence to date for superior group performance, although rare, comes from groups working on relatively complex tasks (13, 46, 50, 51); however, the fact that task complexity was not varied systematically within a single study represents a major source of uncontrolled variation in past research (17, 36).
Third, our analysis of how interacting groups and independent individuals differ in the time they spend during various parts of the problem-solving process offers insight into how group processes could be improved. For example, our finding that groups spend more time in deciding that a task has been completed (i.e., achieving consensus) suggests that assigning a group leader with the ability to unilaterally make that decision, as an individual does, should reduce this source of delay, thereby improving group performance. Moreover, our finding that interacting groups are less likely to submit their best-found solution suggests that storing their best solutions so that they can be reloaded and potentially modified in subsequent steps (a ubiquitous feature of personal productivity software) should also improve their performance (46).
Fourth, our analysis of the solution dynamics of groups vs. individuals provokes additional puzzles for future work. In particular, if groups generate more solutions faster and more efficiently over a wider range of the solution space than even the highest-scoring individuals, why do they not find better solutions?
Finally, we conclude that the science of group performance would benefit from a deeper, more systematic appreciation of the similarities and differences among the tasks that groups are asked to perform, both in the laboratory and in field settings. There is a need for a comprehensive, empirically grounded theory of group tasks (12). A research program that systematically varied task types along with allowed group processes and other contextual factors would advance the basic science of group problem solving while also addressing practical applications.
Materials and Methods
The study was reviewed by the Microsoft Research Ethics Advisory Board and approved by the Microsoft Research Institutional Review Board (MSR IRB; Approval 0000019). All participants provided explicit consent to participate in this study, and the MSR IRB approved the consent procedure. Our experimental design, sample size, and analyses comparing performance across interacting groups and nominal groups were preregistered before the collection of the data (AsPredicted 13123). All other analyses are exploratory.
Algorithmic Solver.
We modeled each room assignment problem as a mixed-integer programming problem and generated the run time for computers to solve each problem using the IBM ILOG CPLEX Optimization Studio software, which is a high-performance mathematical programming solver for linear programming, mixed-integer programming, and quadratic programming. The software ran on a laptop with an Intel Core i5 microprocessor operating at a speed of 2.6 GHz. We ran the software using the default configuration of parameters. The unit of the run time in the task file is “ticks,” which is CPLEX’s unit to measure the amount of work done. The correspondence of ticks to clock time varies across platforms (including hardware, software, machine load, etc.), but given a mixed-integer programming problem and the parameter settings, the ticks needed to solve a problem are deterministic. In this sense, the test–retest reliability of the algorithmic solver is 1. See SI Appendix, section 1.4.2, for additional detail.
Statistical Analysis.
Because each interacting group (or individual) completed the five room assignment tasks, we conducted tests for differences across conditions at the task level. For interaction effects, we modeled the data using a generalized linear mixed model for each outcome (e.g., score, duration, and efficiency) with a random effect for the group or individual identifier. These models account for the nested structure of the data. All statistical tests were two-tailed (as per our preregistration). Details of the statistical tests are in SI Appendix, section S7.
Standardized Coefficients.
To enable meaningful comparisons of effect sizes across tasks of different complexity levels, we standardize various metrics of performance (e.g., score, duration, efficiency, and number of solutions) within each complexity level. For example, the standardized value of measurement X, measured for task instance i of complexity c, is defined aswhere is defined as the mean of X across all instances of the task at complexity c (for interacting and nominal groups), and is the SD.
Data Availability
Replication data and code are available at the Harvard Dataverse, https://doi.org/10.7910/DVN/RP2OCY (52). The experiment was developed using the Empirica platform (53). The source code for the room assignment task can be found at https://github.com/amaatouq/room-assignment-csop, and the source code for the Reading the Mind in the Eyes test can be found at https://github.com/amaatouq/rme-test.
Acknowledgments
We thank Valery Yakubovich, Hazhir Rahmandad, and James Houghton for their helpful discussions and feedback. The authors gratefully acknowledge the Alfred P. Sloan Foundation (G-2020-13924) for financial support.
Footnotes
Author contributions: A.A., M.Y., and D.J.W. designed research; A.A., M.Y., and D.J.W. performed research; A.A., M.A., M.Y., and D.J.W. contributed new reagents/analytic tools; A.A., M.A., M.Y., and D.J.W. analyzed data; and A.A., M.A., M.Y., and D.J.W. wrote the paper.
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2101062118/-/DCSupplemental.
This open access article is distributed under Creative Commons Attribution-NonCommercial-NoDerivatives License 4.0 (CC BY-NC-ND).




